Indeterminate Structures -Analysis of Structures-Part-5
In the statically indeterminate structures number of unknowns (support reactions) are more than number of equilibrium equations that can be written. Therefore, the unknowns cannot be found by using only the equilibrium conditions. Conditions of displacement must also be used to compute the Bending Moment, Shear Force and Axial forces. In this article you will find answer to the questions like- How do you analyse indeterminate structures?,What is force method and displacement medod?, What is compatibility Condition?, etc.
I will try to explain it in a simple way so that the people with limited knowledge also can get benefit from this article. However, nature of the content is such that it will not be easy for them to understand it. Advanced level engineering students and those who want to learn this special part of the structural engineering will get benefit from this article.
There are number of methods available for analysing a statically indeterminate structure. Not all methods can be used easily on all types of structures. In the analysis of indeterminate structures first the Bending Moments (B.M.) are found then the support reactions can be found. Following are some of the methods that are widely used in analysis of indeterminate structures:
1. Column Analogy
2. Moment Distribution
3. Least work
4. General
5. Slope Deflection
6. Matrix Approach
1. Column Analogy: In this method the entire structure is considered as a cross section of an analogous column which is called an elastic area. Width of each element of the structure is assigned to be 1/EI. Here, E and I are the elasticity modulus and moment of inertia of the individual element respectively. Then section properties of this elastic area is determined as usual.
The indeterminate structure is cut at its support to make it determinate. Moment diagram is constructed using applied load on this determinate structure. This determinate moment diagram is applied at elastic area as a load.
In the similar way cross section of any eccentrically loaded column has total stress equals to axial stress plus two bending stresses, the elastic area has them too. These resulting stresses, one axial (𝝈a) and two bending stresses (𝝈x and 𝝈y), of the analogous column are determined. These resulting stresses of the analogous column are the corrective moments that needs to be added to the determinate moments to get the actual B.M. in the indeterminate structure. Using these moments, we can find the reactions at the support where the structure was cut.
2. Moment Distribution: In this method joints of a member is clamped so that they cannot rotate. The fixed end moments for this case is found from standard tables. Then the joint is released one at a time and clamp it again. In this state the joint will rotate and distribution of moment about this point occurs. Some part of change in the moment will be carried over into other joint of the member. Algebraic summation of moments at the support is prepared. Depending on connecting member's stiffness and length part of the new moment at the support is distributed to other connecting members.
This procedure is followed in each joint of the structure. Then the whole process is repeated until the difference in moment at a joint, in connecting members, is close to zero. The resulting moment in the joint is the final bending moment at the joint of an indeterminate structure. In order to find the field moment, the B.M. at field calculated using joint moments at two ends of the member is deducted from the total B.M. for a simply supported member.
3. Least Work: This method is based on the fact that, structure deforms due to application of a load in such a way that the work done by the internal forces in deforming cross section is minimum. In this method the structure is cut to make it determinate. The moments or forces become the redundants or unknowns. Then an equation for the internal work done is written in terms of these unknowns. The first derivative of this equation is then set to zero to find the unknown.
4. General: In this method the indeterminate structure is cut at the redundant (unknown) force then opening of this gap, due to applied load, is determined. is determined. Different methods are available to find the deflection. Some of them are listed below:
a. Area Moment
b.Conjugate Beam
c. Virtual Work
d. Successive Integration
e. Castigliano's Theorem, etc.
After determination of the gap a redundant force is applied to close this gap. Using this redundant force and the applied loads a B.M. diagram for the indeterminate structure can be prepared. Here redundant force is the force which cannot be calculated using the static equilibrium equations.
When there are more than one redundant, all element of the structure is cut at these redundant forces then close the gaps simultaneously, Then prepare the B.M. diagram for the indeterminate structure.
5. Slope Deflection: The Slope Deflection equations give the relation between the B.M. acting on a structural member and the displacements of the member at its ends. When we say displacements it refers to both rotations (ϕ) and deflections (𝜟). In the similar way, as we find the redundant forces and moments in the General method, we can solve for the unknown deflections and rotations at the joints. Using these parameters the end moments can be determined and these are combined with the bending moments due to the given loads.
I have explained all these methods in very briefly. With this information, other dedicated texts can be studied for more details. It's possible that I will be posting more details on these methods later.
With the development of information technology, now a days, different computer software and free applications are available for analysis of the indeterminate or determinate structures. Therefore, manual calculation on these methods are rarely required now.
However, it is important to understand the basics about how these computer programs work. I am trying to explain this approach using the following Matrix method of structural analysis.
6. Matrix Approach for Structural Analysis: Most of the structural analysis software works based on the matrix approach. This approach can be used in all types of structures, including large structures with a high degree of indeterminacy. Solution using the matrix approach involves inversion of the stiffness or flexibility matrix.
Basically, we will discuss about two main methods here that are used in the matrix method, i.e., Force method and Displacement Methods. Prior to explain these methods I need to explain the following two types of indeterminacies:
Degree of static indeterminacy: Degree of static indeterminacy is number of additional equations that are required to solve an indeterminate structure. This is also called degree of redundancy. For example the degree of indeterminacy is two in the following figure. From the static equilibrium perspective, the two roller supports are unnecessary in the Real structure.
Kinematic indeterminacy: A structure is said to be kinematically indeterminate when the displacement component of its joints, such as rotation at the supports, cannot be determined by Compatibility Equations (equation of net displacement) only. In the similar way, we need to use additionally the compatibility equations for solving the statically indeterminate structures, the Equations of Static Equilibrium is required additionally to solve the kinematically indeterminate structures.
 |
| Redundants (M) from supports A and B removed |
Force method: In this method the degree of static indeterminacy of the structure is determined first of all. Then redundants are identified. Here, the moments at supports A and B are the redundant forces. When I say forces, it could be a force or moment. When all redundants are removed from the real structure and the structure is made statically just stable then the resulting structure becomes a determinate structure which is called a released structure or a basic determinate structure. The structure on the right hand side in the above mentioned figure is a released structure. When we put hinges at supports B and A the structure becomes determinate. In this case the spans AB and BC will act as a simply supported beams.
Then a coordinate is assigned to each redundant in the released structure. Thus P1 and P2.....Pn are the redundant at coordinates (1), (2)....(n). In this method we need to maintain the condition of compatibility for displacement .
Compatibility Condition of displacement is, Net displacement at any point in a determinate structure is the sum of displacement in the released (determinate) structure due to the applied loads and the redundant forces. In this case the redundant forces are the released moments.
⟮𝜟⟯ = ⟮𝜟L⟯ + ⟮𝜟R⟯
Total displacement at each redundant is zero as the supports B and A do not settle, in this example. Applying all these conditions, we can write a the following equations in the form of matrix.
 |
| Redundant forces in terms of displacements |
The force vector is made of redundant forces, which are released moments in this example. The flexibility matrix is created by applying an unit force in the released structure and calculating the associated displacement at each coordinate that was assigned earlier. The displacement vector, on the other hand, is created by applying the applied load on the released structure.
Thus, solving the matrix equation the redundants are calculated without knowing the reactions. The calculated redundants are the actual redundants in the indeterminate structure. After this, the support reactions can be calculated using the condition of equilibrium.
In this example, force vector will have two elements, i.e., P1 and P2, the flexibility matrix will have 2x2 elements,i.e., 𝛿11, 𝛿12, 𝛿21,𝛿22. Similarly, the displacement vector will have two elements too, i.e., 𝜟1 and 𝜟2. We use inverse of flexibility matrix in the force method. After solving the matrix equation we will find values of P1 and P2 forces which is actual Bending moments at supports B and A respectively in the indeterminate structure.
As discussed earlier, in order to solve the indeterminate structures, we need to use displacements in addition to the conditions of equilibrium. Thus in the analysis of indeterminate structures, we first calculate the redundants using the compatibility conditions (displacements) then calculate the support reactions using the equations of equilibrium.
Now it will be easier to understand the following:
Force Vector: Released forces, i.e., Redundants at coordinate 1 and 2...
Flexibility matrix: Element of the flexibility matrix 𝛿11 and 𝛿21.... are the displacements at coordinate (point) 1 due to unit redundant P1 and displacements at coordinate (point) 2 due to unit redundant P1. Similarly, 𝛿12 and 𝛿22.... are the displacements at coordinate (point) 1 due to unit redundant P2 and displacements at coordinate (point) 2 due to redundant unit P2.... and so on.
An element of Flexibility matrix shows the amount of displacement at one point in the released structure caused by a unit force (redundant).
Displacement Vector: Elements of displacement vector, 𝜟1 and 𝜟2.... are the deflection at coordinates (points) 1 and 2 due to the applied load on the released structure in this example and so on.
Stiffness Matrix: Inverse of flexibility matrix is called a Stiffness matrix. An element of Stiffness matrix shows the amount of Force (redundant) at one point that is required to cause an unit displacement at a point in the released structure.
Displacement method: This method is similar to the force method but works with unit displacement. In this method the degree of kinematic indeterminacy is determined first. In other words, in how many places the displacement components cannot be determined using only the compatibility equations. Then to each independent displacement component, such as rotation at a support, a coordinate is assigned. Here, the displacement at support and joint at the same support are two independent displacement components.
The points 1,2,...n are the coordinates assigned to each independent displacement components 𝜟1,𝜟2,...𝜟n. In this method firstly, the joints and the supports are restrained from any displacements, all joints and supports are locked. In this case there are no displacements at all, neither at joints nor at the supports. This structure is called a Restrained Structure. Therefore, at the restrained structure the independent displacement components 𝜟1,𝜟2,...𝜟n are zero. For this to happen, forces P1', P2',...Pn' are required at coordinates 1,2,...n.
 |
 |
| Independent displacement component and assigned Coordinate |
 |
| Independent displacement component |
Next, all the joints and supports are released/ unlocked permitting displacements 𝜟1,𝜟2,...𝜟n at points 1,2,..n. For this to happen, forces P1𝜟,P2𝜟,..Pn𝜟 must act at points 1,2,..n respectively. If P1,P2,..Pn are the external forces acting at points 1,2,..n coordinates, then following the condition of static equilibrium,
Pn = Pn'+Pn𝜟
Which is, ⟮P⟯=⟮P'⟯ + ⟮P𝜟⟯
Using the stiffness,
Pn = Pn' + kn1.𝜟1 + kn2.𝜟2 + ... + knn.𝜟n
With this, the equation becomes shortly, ⟮P⟯=⟮P'⟯ + ⟮k⟯ ⟮𝜟⟯ in a matrix form
and then, ⟮𝜟⟯=⟮k⟯⁻¹ {⟮P⟯-⟮P'⟯}
If the external forces P1,P2,...Pn act only at coordinates then,
⟮𝜟⟯=⟮k⟯⁻¹ ⟮P⟯
If there are no external forces P1,P2,..Pn then,
⟮𝜟⟯= - ⟮k⟯⁻¹ ⟮P'⟯
When we expand the matrix,
 |
| Displacement in terms of restraining forces P' |
Knowing the rotations at the real structure, the B.M. at the supports C and B can be calculated directly using the slope deflection method.
Transformation Matrix: In the methods explained above, the flexibility and stiffness matrices were prepared by considering the structure as a whole. In these methods there are chances of making mistakes in calculations of elements for these matrices.
Method of transformation matrix is a more general method for preparation of these matrices which uses the stiffnesses and and flexibilities of individual members (constituent elements) by introducing the use of special matrix which is called Transformation Matrix.
Hence, the matrices of the entire structural system, ⟮𝛿⟯ and ⟮𝜟L⟯, can be prepared from flexibilities of the constituent elements (individual elements) by using the force transformation matrices. In the same way the stiffness matrix, ⟮k⟯, of the entire structural system can be prepared by using the displacement transformation matrix.
In this element approach the matrices for the entire structural system are generated from respective matrices of the constituent elements. This approach is a general approach and consumes significant time if carried out manually. Because of the reason this method is a general method, computer programs use this approach in analysis of structures.
The element coordinates 1*,2*,...m* assigned at constituent elements for preparation of matrices of constituent elements are not necessarily equal to the system coordinates (1,2,...n), i.e., the assigned coordinates to the redundants which are released in the force method.
As we already know, matrix ⟮P⟯ is the redundant forces that are released from the indeterminate structure to create a basic determinate (released) structure. With release of the redundants we obtain displacements ⟮𝜟L⟯ and ⟮𝜟R⟯ at the system coordinates due to applied loads and the redundant respectively.
Displacements and forces at the system coordinates due to applied loads and redundants are as follow:
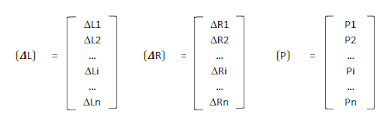 |
| Equations based on system coordinates |
Similarly, the displacements and forces at the element coordinates due to applied loads and redundants are as follow:
 |
| Equations based on element coordinates |
Relationship between Redundant forces at system coordinates, ⟮P⟯ and the forces in the released structure at element coordinates, ⟮P*R⟯ is shown in the following equations:
⟮𝛿*⟯ and ⟮𝛿⟯ are flexibility matrices related to element coordinates and system coordinates respectively.
Similarly, for displacement method the stiffness matrix,
⟮k⟯=⟮d⟯T ⟮k*⟯ ⟮d⟯
Where ⟮k*⟯ and ⟮k⟯ are stiffness matrices related to element coordinates and system coordinates respectively.
Here, element of displacement matrix, di*j shows the displacement at element coordinate i* due to a unit displacement at system coordinate j.
With all of the basic information above, I have only introduced the matrix approach of structural analysis. With the help of this information various dedicated books can be read for detailed information.
In this article I have explained how the statically indeterminate structure is analysed. I have also introduced the concept of Matrix approach of structural analysis including the Transformation matrix.
G.S. Pandit and S. P. Gupta describe this approach in detail in their book- structural analysis a matrix approach, Tata McGraw Hill
In the next article I will explain the Structural Stresses under Basics of designing a structure.
Previous Determination of BM, SF and Axial forces



Comments